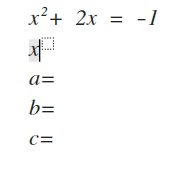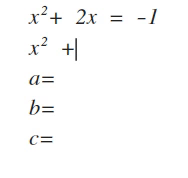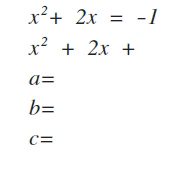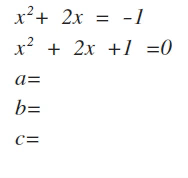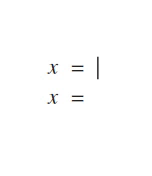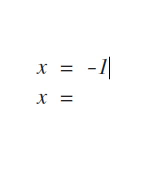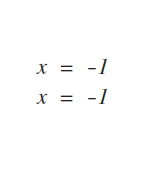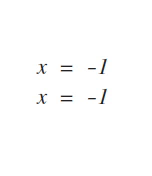Bellow you will find steps and examples for factoring any type of quadratic trinomial. The are listed in increasing order of difficulty, just like IXL.
ax² + bx + c
Level 1: a = 1

Step 1: Find the factors of c (numbers that multiply to equal c) that add up to b.

Step 2: Create binomials with these factors in the form: (variable ± first factor)(variable ± second factor)

ax² + bx + c
Level 2: a = GCF
Steps:
1. Find a greatest common factor for your a , b and c terms.

2. Divide out the GCF from a , b and c.

3. Write out (or mentally think of) the factors of your NEW c term.

4. Choose the factors of c that add up to the NEW coefficient b

5. Write these factors as binomials (x ± first factor)(x ± second factor)

6. Bring down the initial GCF you factored out, and multiply it by your newly created binomials. You’re done!


Level 3: a ≠ 1, but a, b and c have no GCF
Step 1: Draw your factor X and fill in top (with a*c) and bottom (with b).

Step 2: Find the FACTORS of the TOP term (numbers that multiply to equal the top term) that add up to your BOTTOM term. Put these factors on the sides of your X.

Step 3: Take the coefficient, a and multiply it by the variable in your problem. Put this term over the numbers on the sides of your X.

Step 4: Simplify the fractions (if possible).

Step 5: Write factors in binomial form: (numerator +/- denominator) (numerator +/- denominator)

ax² + bx + c
Level 4: a ≠ 1 and a, b and c have a GCF
Step 1: Factor out GCF from a, b and c (if possible)

Step 2: Draw your factor X and fill in top (with a*c) and bottom (with b).

Step 3: Find the FACTORS of the TOP term (numbers that multiply to equal the top term) that add up to your BOTTOM term. Put these factors on the sides of your X.

Step 4: Take the coefficient, a and multiply it by the variable in your problem. Put this term over the numbers on the sides of your X.

Step 5: Simplify the fractions (if possible).

Step 6: Write factors in binomial form: (numerator +/- denominator) (numerator +/- denominator)

Step 7: Bring down the GCF (if you factored one out in step 1) and you’re done!